数据结构与算法(二)——数组、链表
常用数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Tire树(字典树)
线性表结构:数组、链表、栈、队列、散列表
非线性表:二叉树、堆、图、树
线性表(Linear List)是数据排成像一条线一样的结构,每个线性表上的数据最多只有前和后两个方向。
非线性表,数据之间并不是简单的前后关系。
数据结构的特性

数组
数组是一种线性表数据结构;它用一组连续的内存空间,来存储一组具有相同类型的数据。
连续的内存空间、相同的数据类型,所以数组可以随机访问,但对数组进行删除插入,为了保证数组的连续性,就要做大量的数据搬移工作。
数组都是从 0 开始编号的,从数组存储的内存模型上来看,“下标”最确切的定义应该是“偏移(offset)”。
数组适合查找操作,但是查找的时间复杂度并不为 O(1)。
即便是排好的数组,用二分查找,时间复杂度也是O(logn)。
数组支持随机访问,根据下标随机访问的时间复杂度为 O(1)。
优点:简单易用,查找快
缺点:大小固定,增删慢
数组如何实现下标随机访问?
例:长度为 10 的 int 类型的数组 int[] a = newint[10],计算机给数组 a[10],分配了一块连续内存空间 1000~1039,其中,内存块的首地址为 base_address =1000。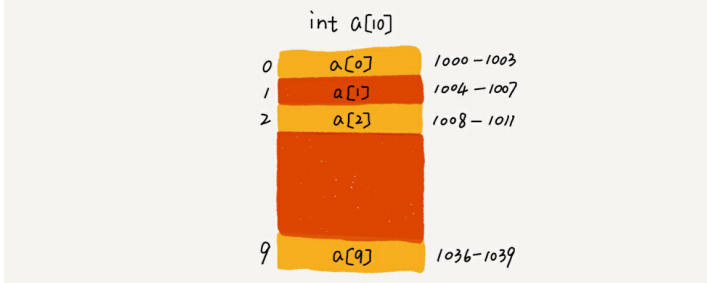
计算机会给每个内存单元分配一个地址,计算机通过地址来访问内存中的数据。当计算机需要随机访问数组中的某个元素时,它会首先通过下面的寻址公式,计算出该元素存储的内存地址:
$$a[i]_address = base_address + i * data_type_size$$
data_type_size 表示数组中每个元素的大小。
容器的优劣
相比于数组,java 中的 ArrayList 将很多数组操作的细节封装起来,并支持动态扩容。一旦超过存储容量,扩容时比较耗内存,因为涉及到内存申请和数据搬移。
数组适合的场景
1.Java ArrayList 的使用涉及装箱拆箱,有一定的性能损耗,如果特别关注性能,可以考虑数组
2.若数据大小事先已知,并且涉及的数据操作非常简单,可以使用数组。
3.表示多维数组时,数组往往更加直观。
4.业务开发容器即可,底层开发,如网络框架,性能优化。选择数组。
链表
从内存结构来看,链表的内存结构是不连续的内存空间,是将一组零散的内存块串联起来,从而进行数据存储的数据结构。
链表通过指针将一组零散的内存块串联在一起,内存块称为链表的“结点”(Node 存储数据、记录链上的下一个结点的地址),后继指针(next)用来记录下个结点地址的指针。
优点:增删快 O(1),支持动态扩容
缺点:查找慢 O(n),内存空间消耗大,频繁增删,容易造成冗余
三种最常见的链表结构:单链表、双向链表和循环链表
单链表
每个节点只包含一个指针,即后继指针。
单链表有两个特殊的节点,即头节点和尾节点。
头结点用来记录链表的基地址,尾结点指向一个空地址 NULL,表示这是链表上最后一个结点。
循环链表
除了尾节点的后继指针指向首节点的地址外均与单链表一致。
适用于存储有循环特点的数据,比如约瑟夫问题。
双向链表
节点除了存储数据外,还有两个指针分别指向前一个节点地址(前驱指针 prev)和下一个节点地址(后继指针 next),首节点的前驱指针 prev 和尾节点的后继指针均指向空地址
双向循环链表
首节点的前驱指针指向尾节点,尾节点的后继指针指向首节点
比较
| 时间复杂度 | 数组 | 链表 |
|---|---|---|
| 随机访问 | $$O(1)$$ | $$O(n)$$ |
| 插入删除 | $$O(n)$$ | $$O(1)$$ |
应用
LRU 缓存策略
缓存是一种提高数据读取性能的技术。
缓存的大小是有限的,当缓存被用满时,哪些数据应该被清理出去,哪些数据应该被保留?就需要用到缓存淘汰策略。
缓存淘汰策略是当缓存被用满时清理数据的优先顺序。
常见的三种缓存淘汰策略
先进先出策略 FIFO(First In,First Out)、最少使用策略 LFU(Least Frenquently Used)、最近最少使用策略 LRU(Least Recently Used)。
链表实现 LRU
当访问的数据没有存储在缓存的链表中时,直接将数据插入链表表头,时间复杂度为O(1);
当访问的数据存在于存储的链表中时,将该数据对应的节点,插入到链表表头,时间复杂度为O(n)。
如果缓存被占满,则从链表尾部的数据开始清理,时间复杂度为O(1)。
PS:维护一个有序链表,尾部为最早访问的数据,头部为最新,现插入一数据
1.遍历,查看数据是否存在
2.1 存在,删除已有数据,将数据插入到头部
2.2 不存在
2.2.1 链表没满,直接插入到头部
2.2.2 链表满了,删除链表尾节点,将数据插入头部
数组实现 LRU
1.首位置保存最新访问数据,末尾位置优先清理
当访问的数据未存在于缓存的数组中时,直接将数据插入数组第一个元素位置,此时数组所有元素需要向后移动1个位置,时间复杂度为O(n);
当访问的数据存在于缓存的数组中时,查找到数据并将其插入数组的第一个位置,此时亦需移动数组元素,时间复杂度为O(n)。
缓存用满时,则清理掉末尾的数据,时间复杂度为O(1)。
2.首位置优先清理,末尾位置保存最新访问数据
当访问的数据未存在于缓存的数组中时,直接将数据添加进数组作为当前最有一个元素时间复杂度为O(1);
当访问的数据存在于缓存的数组中时,查找到数据并将其插入当前数组最后一个元素的位置,此时亦需移动数组元素,时间复杂度为O(n)。
缓存用满时,则清理掉数组首位置的元素,且剩余数组元素需整体前移一位,时间复杂度为O(n)。
(优化:清理的时候可以考虑一次性清理一定数量,从而降低清理次数,提高性能。)
链表回文串验证
使用快慢两个指针找到链表中点,慢指针每次前进一步,快指针每次前进两步。在慢指针前进的过程中,同时修改其 next 指针,使得链表前半部分反序。最后比较中点两侧的链表是否相等。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isPalindrome(ListNode head) {
if (head == null || head.next == null) {
return true;
}
ListNode prev = null;
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
ListNode next = slow.next;
slow.next = prev;
prev = slow;
slow = next;
}
if (fast != null) {
slow = slow.next;
}
while (slow != null) {
if (slow.val != prev.val) {
return false;
}
slow = slow.next;
prev = prev.next;
}
return true;
}
}
时空替换思想
时空替换思想:“用空间换时间” 与 “用时间换空间”
当内存空间充足的时候,如果我们更加追求代码的执行速度,我们就可以选择空间复杂度相对较高,时间复杂度小相对较低的算法和数据结构,缓存就是空间换时间的例子。如果内存比较紧缺,比如代码跑在手机或者单片机上,这时,就要反过来用时间换空间的思路。
「空间换时间」某些情况下”双向链表”替代”单向链表”;缓存