图的定义
图(Graph)是一种复杂的非线性表结构。
- 顶点(vertex):图中的元素;
- 边(edge):图中的顶点与其他任意顶点建立连接的关系;
- 顶点的度(degree):跟顶点相连接的边的条数。
- 入度(In-degree)和出度(Out-degree):对于有向图,一个顶点的入度是指以其为终点的边数;出度指以该顶点为起点的边数;
- 图有多种类型,包括有向图、无向图、简单图、多重图、有向图、无向图等;
图的分类
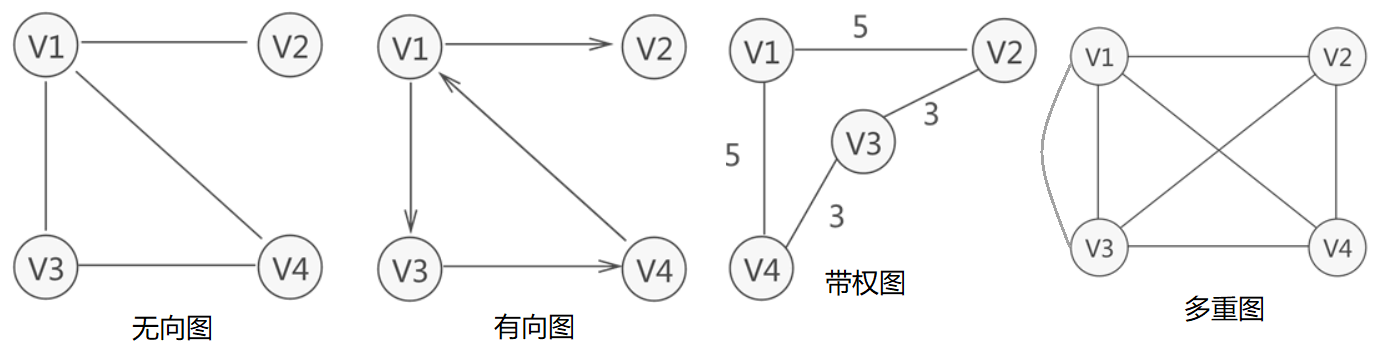
有向图和无向图
图的每条边规定一个方向,那么得到的图称为有向图;相反,边没有方向的图称为无向图。
简单图
- 任意两顶点之间只有一条边(在有向图中为两顶点之间每个方向只有一条边);
- 每条边所关联的是两个不同的顶点
带权图(weighted graph)
在带权图中,每条边都有一个权重(weight)[非负实数]。
多重图
图中某两个顶点之间的边数多于一条,又允许顶点通过同一条边和自己关联,则称为多重图
图的存储
邻接矩阵(Adjacency Matrix)
邻接矩阵是图的常用存储表示,它的底层依赖一个二维数组。它用两个数组分别存储数据元素(顶点)的信息和数据元素之间的关系(边或弧)的信息。
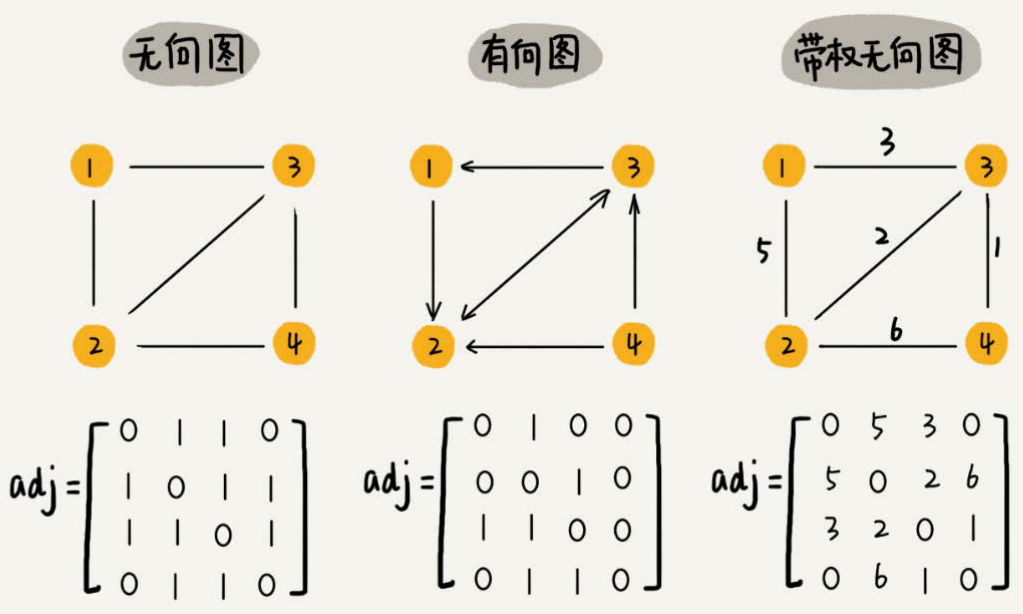
优点:
- 邻接矩阵的存储方式简单、直接,可以高效的获取两个顶点的关系;
- 计算方便。(求解最短路径 Floyd-Warshall 算法)
用邻接矩阵来表示一个图,虽然简单、直观,但是比较浪费存储空间。
- 对于无向图,a[i][j] == a[j][i],我们只需要存储一个就好,在二维数组中,通过对角线可以划分为两部分,我们只要利用其中一部分的空间就可以了,另外一部分则是多余的。
- 存储的是稀疏图(Sparse Matrix):顶点很多,但每个顶点的边并不多,邻接矩阵的存储方法就更加浪费空间了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| public class AMWGraph {
private ArrayList vertexList;
private int[][] edges;
private int numOfEdges;
public AMWGraph(int n) {
edges=new int[n][n];
vertexList=new ArrayList(n);
numOfEdges=0;
}
public int getNumOfVertex() {
return vertexList.size();
}
public int getNumOfEdges() {
return numOfEdges;
}
public Object getValueByIndex(int i) {
return vertexList.get(i);
}
public int getWeight(int v1,int v2) {
return edges[v1][v2];
}
public void insertVertex(Object vertex) {
vertexList.add(vertexList.size(),vertex);
}
public void insertEdge(int v1,int v2,int weight) {
edges[v1][v2]=weight;
numOfEdges++;
}
public void deleteEdge(int v1,int v2) {
edges[v1][v2]=0;
numOfEdges--;
}
public int getFirstNeighbor(int index) {
for(int j=0;j<vertexList.size();j++) {
if (edges[index][j]>0) {
return j;
}
}
return -1;
}
public int getNextNeighbor(int v1,int v2) {
for (int j=v2+1;j<vertexList.size();j++) {
if (edges[v1][j]>0) {
return j;
}
}
return -1;
}
}
|
邻接表(Adjacency List)
邻接表与散列表有点类似,点击了解散列表
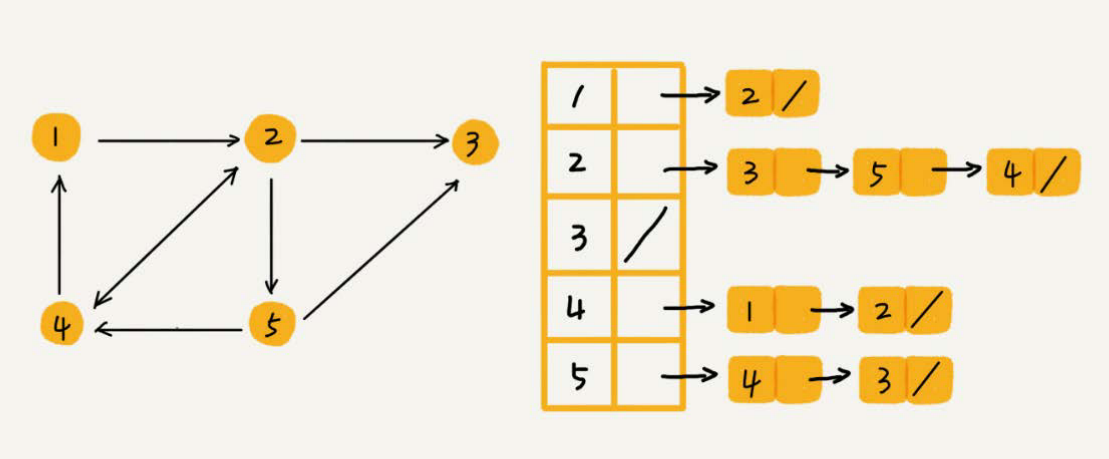
图的顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。
邻接表存储起来比较节省空间,但是使用起来就比较耗时间。
当链表过长,为了提高查找效率,我们可以将链表换成其他更加高效的数据结构,如平衡二叉树(红黑树)、跳表、散列表等
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public class Graph {
private int v;
private LinkedList<Integer> adj[];
public Graph(int v) {
this.v = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i) {
adj[i] = new LinkedList<>();
}
}
public void addEdge(int s, int t) {
adj[s].add(t);
adj[t].add(s);
}
}
|
图的遍历
深度优先搜索算法(DFS)
深度优先搜索(Depth-First-Search),类似于树的先序遍历,从图中某个顶点v出发,访问该顶点,然后依次从v的未被访问的邻接点出发继续深度优先遍历图中的其余顶点,直至图中所有与v有路径相通的顶点都被访问完为止。
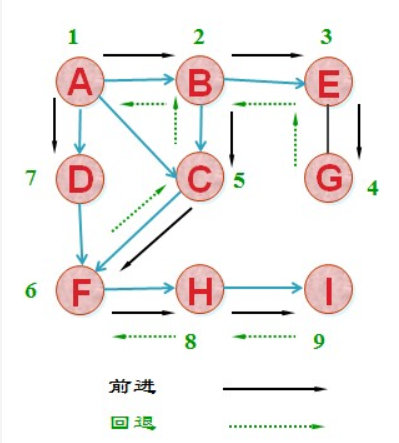
深度优先搜索的时间复杂度为 O(E),E 表示边的个数;空间复杂度为 O(V),V 表示顶点的个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
boolean found = false;
public void dfs(int s, int t) {
found = false;
boolean[] visited = new boolean[v];
int[] prev = new int[v];
for (int i = 0; i < v; ++i) {
prev[i] = -1;
}
recurDfs(s, t, visited, prev);
print(prev, s, t);
}
private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
if (found == true) return;
visited[w] = true;
if (w == t) {
found = true;
return;
}
for (int i = 0; i < adj[w].size(); ++i) {
int q = adj[w].get(i);
if (!visited[q]) {
prev[q] = w;
recurDfs(q, t, visited, prev);
}
}
}
|
广度优先搜索算法(BFS)
广度优先搜索(Breadth-First-Search),一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。
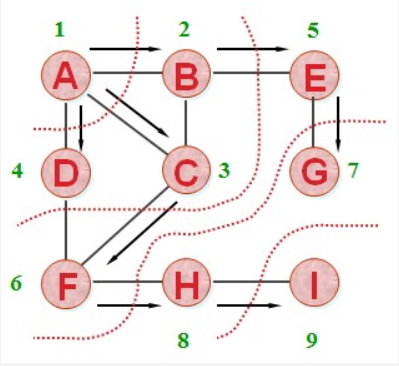
广度优先搜索的时间复杂度为 O(E),,E 表示边的个数;空间复杂度为 O(V),V 表示顶点的个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| public void bfs(int s, int t) {
if (s == t) return;
boolean[] visited = new boolean[v];
visited[s]=true;
Queue<Integer> queue = new LinkedList<>();
queue.add(s);
int[] prev = new int[v];
for (int i = 0; i < v; ++i) {
prev[i] = -1;
}
while (queue.size() != 0) {
int w = queue.poll();
for (int i = 0; i < adj[w].size(); ++i) {
int q = adj[w].get(i);
if (!visited[q]) {
prev[q] = w;
if (q == t) {
print(prev, s, t);
return;
}
visited[q] = true;
queue.add(q);
}
}
}
}
private void print(int[] prev, int s, int t) {
if (prev[t] != -1 && t != s) {
print(prev, s, prev[t]);
}
System.out.print(t + " ");
}
|




