快排、归并排序都使用到了分治思想。
分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题 来解决。小的子问题解决了，大问题也就解决了。
分治思想跟递归思想很像，一般用递归来实现的。
分治是一种解决问题的处理思想，递归是一种编程技巧。

快排排序（Quick Sort）

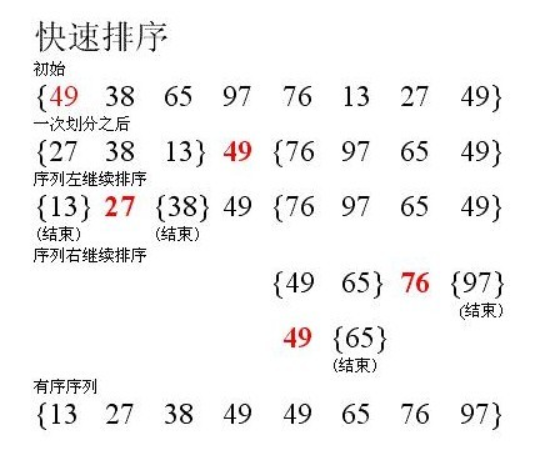
快排排序算法的操作如下：

  1. 挑选基准值：从数列中挑出一个元素，称为“基准”（pivot）;
  2. 分割：重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（与基准值相等的数可以到任何一边）。在这个分割结束之后，对基准值的排序就已经完成;
  3. 递归排序子序列：递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class Application {

    public static void qSort(int[] arr, int head, int tail) {
        if (head >= tail || arr == null || arr.length <= 1) {
            return;
        }
        int i = head, j = tail, pivot = arr[(head + tail) / 2];
        while (i <= j) {
            while (arr[i] < pivot) {
                ++i;
            }
            while (arr[j] > pivot) {
                --j;
            }
            if (i < j) {
                int t = arr[i];
                arr[i] = arr[j];
                arr[j] = t;
                ++i;
                --j;
            } else if (i == j) {
                ++i;
            }
        }
        qSort(arr, head, j);
        qSort(arr, i, tail);
    }

    public static void main(String[] args) {
        int[] arr = new int[]{1, 4, 8, 2, 55, 3, 4, 8, 6, 4, 0, 11, 34, 90, 23, 54, 77, 9, 2, 9, 4, 10};
        qSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }
}

优化

  1. 三数取中法
    我们从区间的首、尾、中间，分别取出一个数，然后对比大小，取这 3 个数的中间值作为分区点。
  2. 随机法
    随机法就是每次从要排序的区间中，随机选择一个元素作为分区点。

归并排序（Merge Sort）

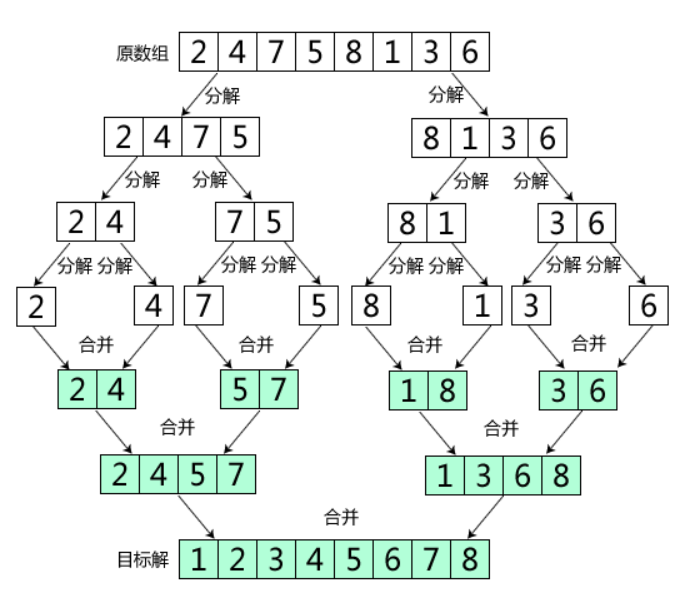
归并排序算法(递归法)的操作如下：

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  4. 重复步骤 3 直到某一指针到达序列尾；
  5. 将另一序列剩下的所有元素直接复制到合并序列尾。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 归并排序算法 
static void merge_sort_recursive(int[] arr, int[] result, int start, int end) {
	if (start >= end)
		return;
	int len = end - start, mid = (len >> 1) + start;
	int start1 = start, end1 = mid;
	int start2 = mid + 1, end2 = end;
	merge_sort_recursive(arr, result, start1, end1); //左边排序
	merge_sort_recursive(arr, result, start2, end2); //右边排序
	int k = start;
	while (start1 <= end1 && start2 <= end2)
		result[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
	while (start1 <= end1)
		result[k++] = arr[start1++];
	while (start2 <= end2)
		result[k++] = arr[start2++];
	for (k = start; k <= end; k++)
		arr[k] = result[k];
}

public static void merge_sort(int[] arr) {
	int len = arr.length;
	int[] result = new int[len];
	merge_sort_recursive(arr, result, 0, len - 1);
}

总结

原地排序 稳定的排序算法 最好 最坏 平均
快速排序 是 不是 $$O(nlogn) O(n^2) O(nlogn)$$
归并排序 不是 是 $$O(nlogn) O(nlogn) O(nlogn)$$