数据结构与算法(九)——红黑树(Red Black Tree)
性质
- 红黑树是一种自平衡二叉查找树(BST)
- 节点非黑即红,根节点是黑色的;
- 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
自平衡二叉树
AVL树(经典平衡树, 所有操作的最坏复杂度都是 O(log n))、Treap、伸展树、红黑树、替罪羊树、AA树、加权平衡树等
红黑树相对于AVL树来说,牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树。
操作
插入
红黑树规定,插入的节点必须是红色的。而且,二叉查找树中新插入的节点都是放在叶子节点上。
红黑树插入调整的基础操作:左右旋转和改变颜色。
情况1:插入节点位于树的根上,没有父节点。直接改变它的颜色,把它变成黑色就可以了。
情况2:插入节点的父节点是黑色的,直接插入就行了。
情况3:如图 N 为红,P 为红,(祖节点一定存在,且为黑,下边同理)U 也为红,这里不论 P 是 G 的左孩子,还是右孩子;不论 N 是 P 的左孩子,还是右孩子。
操作:把 P、U 改为黑色,G 改为红色,如 G 为根节点进行情况1操作,否则进行情况4和情况5
解析:N、P 都为红,违反性质4;若把 P 改为黑,符合性质4,显然右边少了一个黑节点,违反性质5;所以我们把G,U都改为相反色,符合性质5,违反性质2;将 G 作为关注点,进行下一步操作。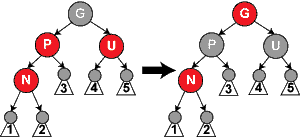
情况4:N 为红,P 为红,U 为黑,P 为 G 的左孩子,N 为 P 的右孩子(或者 P 为 G 的右孩子,N 为 P 的左孩子;反正两方向相反)。
操作:需要进行两次变换(旋转),图中只显示了一次变换—–首先 P、N 变换,颜色不变;然后就变成了情况5的情况,按照情况4操作,即结束。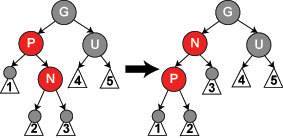
情况5:N 为红,P 为红,U 为黑,P 为 G 的左孩子,N 为 P 的左孩子(或者 P 为 G 的右孩子,N 为 P 的左孩子;反正就是同向的)。
操作:P、G 变色,P、G 变换即左左单旋(或者右右单旋),结束。
删除
如果需要删除的节点有两个儿子,那么问题可以被转化成删除另一个只有一个儿子的节点的问题,下面只讨论删除只有一个子节点的问题
情况2-6图中,N 都是是删除了黑色节点后替换上来的子节点
情况1:要删除 N ,N 为根节点,直接删除,新的根节点为黑色。
情况2:S 为红色(那么父节点 P 一定是黑,子节点一定是黑),N 是 P 的左孩子(或者 N 是 P 的右孩子)。
操作:以 P 为中心左旋,S 变为祖节点,P、S 颜色对调,违法性质5,未结束,接下来按情况4、情况5或情况6来处理。
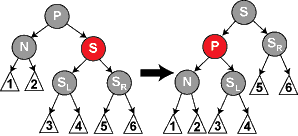
情况3:P、S 及 S 的孩子们都为黑。
操作:S 改为红色,接着按情况2做处理。
情况4:P 为红(S 一定为黑),S 的孩子们都为黑。
操作:P变为黑,S改为红,结束。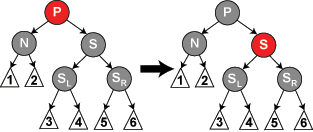
情况5:P 任意色,S 为黑,N 是 P 的左孩子,S 的右孩子 SR 为红,S 的左孩子任意(或者是 N 是 P 的右孩子,S 的左孩子为红,S 的右孩子任意)。
操作:SR(SL)改为黑,P 改为黑,S 改为 P 的颜色,p 左旋,结束。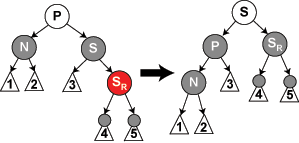
情况6:S 为黑,S 的左孩子 SL 为红,S 的右孩子 SR 为黑(或者 S 的右孩子为红,S 的左孩子为黑)。
操作:SL(或SR)改为黑,S 改为红,SL(SR)、S 右旋(左旋);此时就回到了情况5,SL(SR)变成了黑 S,S 变成了红。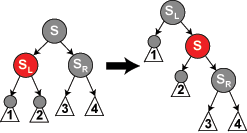
应用
java 中的 treeMap
JDK1.8中 HashMap 在单链表冲突后采用红黑树提高查找插入的效率